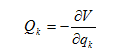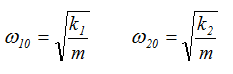osilasi

Bab III.  Teori Getaran Dengan Amplitudo Kecil

               Dan Osilator Tergandeng                              

 

1. ENERGI KESETIMBANGAN DAN ENERGI POTENSIAL

Untuk memahami secara mendasar teori getaran, perlu dikaji terlebih dahulu hubungan antara energi potensial dan energi kesetimbangan yang menuju ke keadaan stabil atau keadaan tak stabil dari sistem yang ditinjau. Untuk maksud tersebut, marilah kita meninjau sebuah sistem dengan n derajat kebebasan dan konfigurasinya dinyatakan dengan koordinat rampatan q₁, q₁, … q_n.  Selanjutnya, asumsikan bahwa sistem tersebut konservatif; dalam hal ini energi potensial merupakan fungsi dari koordinat rampatan

                                          V = V(q₁, q₁, … q_n)                                  (1)

Energi rampatan Q_k dinyatakan dengan :

k = 1,2, …n                    (2)

Jika sistem yang ditinjau tersebut berada dalam kondisi setimbang, hal ini berarti bahwa semua gaya rampatan Q_k harus sama dengan nol. Kondisi yang harus dipenuhi dalam keadaan setimbang tersebut adalah

Sistem tersebut tetap dalam keadaan setimbang jika tidak ada gaya luar yang bekerja padanya. Misalkan sistem tersebut dipindahkan dari posisi setimbangnya. Setelah dipindahkan, sistem dapat kembali ke keadaan setimbang atau ke keadaan tidak setimbang. Jika setelah mengalami pergeseran sistem tidak kembali ke keadaan kesetimbangan semula, sistem tersebut dikatakan berada dalam kesetimbangan stabil (stable equilibrium). Jika sistem tidak kembali ke keadaan kesetimbangan semula, dinamakan kesetimbangan tak stabil (unstable equilibrium). Sedangkan jika sistem cenderung menjauh dari kesetimbangan semula setelah diberi pergeseran yang cukup kecil, sistem  tersebut berada dalam kesetimbangan netral (neutral equilibrium).

            Marilah kita telaah lebih jauh hubungan antara fungsi energi potensial V dengan kestabilan sebuah sistem. Misalkan dalam keadaan setimbang energi kinetik dan energi potensial sistem masing-masing adalah T_o dan V_o. Jika sistem mengalami pergeseran (dengan memberikan sedikit gaya) energi kinetik dan energi potensial masing-masing menjadi T dan V. Oleh karena energi total sistem kekal, maka

T_o + V_o = T + V

                            T  - T_o  = -(V - V_o)                                     (4)

Misalkan bahwa bentuk grafik energi potensial V dengan koordinat rampatan q adalah seperti yang ditunjukkan pada gambar berikut :

Pada titik A dan B dimana harga  , merupakan titik-titik setimbang. Marilah kita telaah perilaku kesetimbangan pada titik-titik ini.

Misalkan, mula-mula sistem berada dalam kesetimbangan pada titik B dimana energi potensial V_o maksimum. Jika sistem bergeser dari posisi titik kesetimbangan, energinya sama dengan V yang lebih kecil dari harga V_o. Jadi V - V_o negatif, dan T - T_o positif, yang berarti bahwa T bertambah. Oleh karena T  bertambah dengan bertambahnya pergeseran, sistem tidak akan pernah kembali ke

keadaan setimbang B, oleh karena itu titik B merupakan posisi kesetimbangan tak stabil. Sekarang perhatikan titik A yang sistem berada dalam keadaan stabil dengan energi V_o minimum. Jika sistem bergeser dari posisi titik kesetimbangan, energinya sama dengan V yang lebih kecil dari harga V_o. Jadi V - V_o positif, dan T - T_o negatif, yang berarti bahwa T berkurang. Oleh karena T  bertambah dengan bertambahnya pergeseran.Oleh karena T  tidak boleh berharga negatif,  maka harganya akan terus berkurang sampai mendekati  harga nol yang berarti bahwa sistem akan kembali ke keadaan setimbang. Sistem berada dalam kesetimbangan stabil. Kita simpulkan bahwa untuk pergeseran yang cukup kecil  kondisi kesetimbangan stabil  posisi dimana energi potensial V_o adalah minimum pada konfigurasi kesetimbangan. Selanjutnya, pada keadaan setimbang dV/dt sama dengan nol, V-V_o positif, yang berati bahwa d²V/dt² positif pada keadaan setimbang. Sebaliknya, pada posisi kesetimbangan tak stabil, d²V/dt² negatif sebab V - V_o negatif.

Jadi syarat kesetimbangan dapat dinyatakan sebagai berikut :

Kesetimbangan stabil :                                   d²V/dq² > 0      Kesetimbangan tak stabil :                            d²V/dq² < 0                                         

Untuk d²V/dt² = 0 mesti kita periksa pada turunan yang lebih tinggi. Jika turunan pertama tak nolnya adalah ganjil, maka sistem berada dalam kesetimbangan tak stabil. Sebaliknya, jika turunan pertama tak nol adalah genap, maka sistem dapat berada dalam kondisi stabil atau tak stabil bergantung pada nilai turunannya (lebih besar atau lebih kecil nol). Jadi                                

Jika dⁿV/dtⁿ ¹ 0,    n >2 dan ganjil,  sistem tak stabil

Jika dⁿV/dtⁿ > 0,    n >2 dan genap,  sistem stabil

Jika dⁿV/dtⁿ < 0,    n >2 dan genap,  sistem tak stabil

Contoh :

Tunjukkan bahwa batang pemukul dengan panjang l yang tergantung pada titik O dan pusat massanya berada sejauh d dari O adalah berada dalam posisi kesetimbangan stabil.

Penyelesaian : Untuk membahasnya, perhatikan gambar 2. Ketika batang pemukul menyimpang , garis OC membuat sudut q dengan garis vertikal. Pusat massanya akan naik setinggi h, sehingga energi potensialnya :

V = mgh = mgd ( 1 - cos q )

Seperti yang ditunjukkan dalam gambar,  q = 0°, jadi :

dV/dq  = mgd sin q

d²V/dq²  = mgd cos q

Jadi untuk q = 0°, dV/dq =0 dan d²V/dq²  = mgd >0 dan sistem berada dalam kesetimbangan stabil.

Sebaliknya jika diletakkan dalam posisi seperti pada gambar 2c,

V = -mgh = -mgd ( 1 - cos q )

Seperti yang ditunjukkan dalam gambar,  q = 0°.

Jadi untuk q = 0°, dV/dq =0 dan d²V/dq²  = -mgd <0 dan sistem berada dalam kesetimbangan tak stabil.

 

Berdasarkan contoh di atas dapat disimpulkan bahwa jika pusat massa berada di bawah titik gantungnya, maka sistem berada dalam kesetimbangan stabil ; dan jika pusat massa berada titik gantungnya, maka sistem berada dalam kesetimbangan tak stabil.

B. OSILATOR BERGANDENG DUA DAN KOORDINAT NORMAL

Contoh sederhana sebuah sistem yang bergandeng adalah dua osilator harmonik yang dihubungkan oleh pegas, seperti yang ditunjukkan dalam gambar 3. Tiap osilator harmonik mempunyai partikel dengan massa m, dan tetapan pegas masing-masing adalah k₁ dan k₂. Keduanya dihubungkan oleh pegas lain yang tetapannya k'. Gerakan kedua massa dibatasi pada sepanjang arah yang menghubungkan kedua massa, misalkan sepanjang sumbu X. Sistem tersebut memiliki dua derajat kebebasan yang dinyatakan oleh koordinat x₁ dan x₂. Konfigurasi sistem dinyatakan dengan pergeseran dari kedudukan setimbang O₁ dan O₂. Pergeseran positif diambil dalam arah kanan dan pergeseran negatif dalam arah kiri. Jika kedua osilator tidak saling digandengkan, maka frekuensi masing-masing adalah :

Jika kedua osilator dihubungkan oleh pegas dengan tetapan k', sistem akan bergetar dengan frekuensi yang nilainya berbeda dari frekuensi yang dinyatakan dalam persamaan (5).

Energi kinetiknya adalah

  

dan energi potensialnya adalah :

Oleh karena itu fungsi Lagrangian dapat ditulis :

Persamaan Lagrange untuk gerak di atas adalah :

Dengan menggunakan kedua persamaan di atas, diperoleh solusi :

Suku ketiga dalam persamaan di atas muncul oleh kedua osilator tergandeng. Jika kedua osilator tidak tergandeng satu sama lain, osilator tersebut akan bergetar dengan frekuensi seperti yang ditunjukkan dalam persamaan (5). Persamaan diferensial pada di atas dapat ditulis :

Kedua persamaan di atas adalah independen seandainya suku ketiga tidak muncul. Hal ini berarti bahwa jika massa kedua dalam keadaan diam x₂ = 0, frekuensi getaran adalah sama dengan frekuensi osilator pertama, dan dari persamaan (12) diperoleh :

Dan jika massa m₁ dalam keadaan diam, x₁ = 0, frekuensi getaran adalah frekuensi osilator kedua 

 Frekuensi dan  adalah lebih besar dari  dan  yang dinyatakan dalam persamaan (5). Alasannya adalah bahwa  tiap massa dihubungkan pada kedua pegas.

Untuk memperoleh mode getaran yang berbeda, kita harus memecahkan secara simultan persamaan diferensial linier orde dua yang dinyatakan dalam persamaan (10) dan (11). Persoalan ini dapat dibuat menjadi sederhana dengan menganggap bahwa kedua osilator benar-benar identik (sama), yakni k₁ = k₂ = k. Jadi persamaan diferensialnya adalah :

Kita mencoba penyelesaian persamaan diferensial di atas dengan mengambil salah satu dari tiga bentuk berikut :

untuk mempelajari selanjutnya, dapat klik disini : osilasi